前回、 枚のトランプを
回パーフェクト・シャッフルしたら元に戻るとき、
と
との間で満たされるべき条件を導きました:
が自然数
「 が与えられたとき、この条件を満たす
を求める」ってのが目標です。
簡単な場合として、 がある自然数
を使って「
」と書けるとき、「
」となります。 例えば、
のとき、4回のパーフェクト・シャッフルで元に戻ります。
一般の場合の  の求め方
の求め方
前回の最後に書いたように、上式を使って一般の 着目する点は、 を2進数で表すと*1
と、「1」が 個並ぶことです。
を求める手順の概要は以下の通り:
を2進数に書き換える
- この2進数を何倍かして「1」のみが並ぶようにする
- 1の個数が求める
一般的な場合を説明するのは大変なので、次節で具体例を計算するにとどめます。
 の場合
の場合
前節の手順に従って、「★Step 1★  を2進数に書き換える
を2進数に書き換える
★Step 2★ この2進数を何倍かして「1」のみが並ぶようにする
ここが一番手間の掛かる計算。 2進数の足し算に慣れればどうってこともないんですが。やることは、「1011」に、「1011」の桁を左にずらしたものをどんどん足していって、最終的に全てが「1」になるようにすることです。 この際、一番右(位が低い)の「0」から順に消していきましょう。 具体的には次のように、筆算で計算すると良いでしょう:
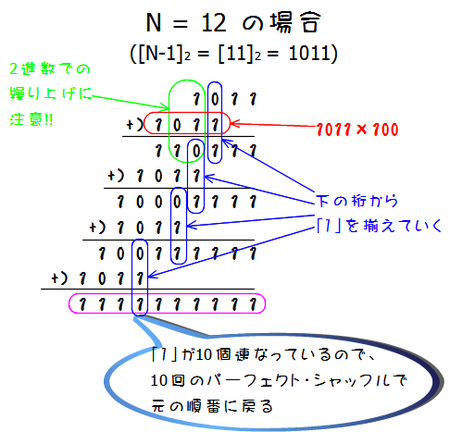
★Step 3★ 1の個数が求める 
「1011」の場合は、最終的に「1」だけになったとき、それが10個連なってました。 よって、どんな  が簡単か?
が簡単か?
一応、まず最初に思いつくのは、既に が「1」のみの場合です。 これは(この記事の最初にも書いた) 「
」と書ける場合です。 これは、桁をずらして足したりする必要がありません。 結果は「
」 となります。
また、その次の偶数「」も比較的簡単に計算できます。 この場合は、
を2進数で表すと「
」(0が
個)となるので、(計算は省きますが)「
」となります。
次に、桁を1つだけずらす様な場合、例えば「10101」のように「1」と「0」が交互になっているような場合です。 結果だけ書くと、「」*2のとき「
」となります。
 の場合
の場合
さて、「ちなみに の場合は
、
の場合は
になりました。 やはり
は特別!