2次曲線：カメラに映る円

『Q.E.D.証明終了(31) (月刊マガジンコミックス)　眼の中の悪魔』に出てきた、ビデオに映る2次曲線の形を数式で確かめてみましょう。　高校数学で理解できます（数学B のベクトルと数学C の2次曲線の知識が必要）

問題設定

円周は xy-平面上（床とする）にあり、中心が原点で半径が $r$ であるとする。　また点 P を円周上の点とする。
観測者（ビデオカメラ）は原点から x の正の方向に 1、高さが $h$ の位置にあるとする。　この点を A とする。

$r < 1$ のときの図を描くと下図のようになります：

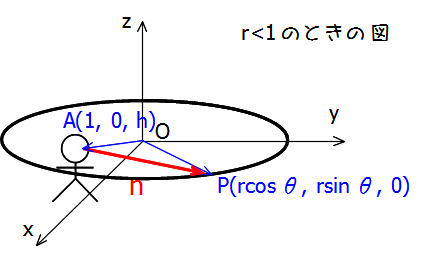
各点の位置ベクトルは以下の通り（ $\theta$ は媒介変数）：

$\vec{OP} = \left( r\cos\theta \\ r\sin\theta \\ 0\right),\qquad \vec{OA} = \left( 1 \\ 0 \\ h \right)$

解法の流れ

解法の大まかな流れは以下のようになります：

観測者に対する円周上の点への位置ベクトルを求める（ $\vec{n}$ とする）
$\vec{n}$ を「仮想スクリーン上」へ射影する（ $\vec{n}_{\rm\tiny proj}$ とする）
$\vec{n}_{\rm\tiny proj}$ の y, z 座標から媒介変数 $\theta$ を消去して、仮想スクリーン上の軌跡を求める

観測者に対する円周上の点への位置ベクトル $\vec{n}$

求めるベクトルは、始点が A、終点が P のベクトルです：

$\vec{n} = \vec{OP} - \vec{OA} = \left( r\cos\theta -1 \\ r\sin\theta \\ -h \right)$

「仮想スクリーン上」へ射影されたベクトル $\vec{n}_{\tiny \rm proj}$

点 A に対する点 P の位置ベクトル $\vec{n}$ を「画面上の位置ベクトル」に変えるために、観測者の前方（ $x$ の負の方向）に1だけ離れた位置に仮想スクリーンを考え、そこに $\vec{n}$ を射影 (projection) しましょう。

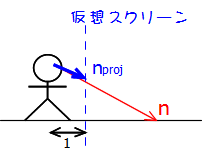
この変換は、 $\vec{n}$ の $x$ 成分が -1 になるように $\vec{n}$ を実数倍することで実現できます。　つまり、全成分を $1-r\cos\theta$ で割ってあげます：

$\vec{n}_{\tiny \rm proj} = \left( -1 \\ \frac{r\sin\theta}{1-r\cos\theta} \\ -\frac{h}{1-r\cos\theta} \right)$

▲注意

$r \ge 1$ のときは、観測者の真下と後方（ $x$ の正の方向）を除かなくてはいけないので、
$r\cos\theta -1 < 0 \qquad\qquad (1)$
という制限がいります。

仮想スクリーン上の軌跡

$\vec{n}_{\tiny \rm proj}$ より、仮想スクリーン上の軌跡の媒介変数表示は以下のようになります：

$\left\{ y = \frac{r\sin\theta}{1-r\cos\theta} \qquad\qquad (2) \\ z = -\frac{h}{1-r\cos\theta} \qquad\qquad (3)\right.$

これらから媒介変数 $\theta$ を消去すると仮想スクリーン上の軌跡の方程式が得られます。

チョット計算

(2) 式より

$r\cos\theta = \frac{z + h}{z}$

(2), (3) 式より

$r\cos\theta = - \frac{hy}{z}$

したがって

$\left(\frac{hy}{z}\right)^2 + \left(\frac{z + h}{z}\right)^2 = r^2$
$\therefore h^2y^2 + z^2 + 2hz + h^2 = z^2r^2 \qquad\qquad (4)$